10235. Ordering tasks

John has n tasks to do. Unfortunately, the tasks are not independent and the execution of one task is only possible if other tasks have already been executed.

Input. Consist of several instances of the problem. Each instance begins with a line containing two integers: number of tasks n (1 ≤ n ≤ 100), numbered from 1 to n, and number m of direct precedence relations between tasks. After this, there will be m lines with two integers i and j, representing the fact that task i must be executed before task j.

An instance with n = m = 0 will finish the input.

Output. For each instance, print a line with n integers representing the tasks in a possible order of execution.

Sample input	Sample output
6 6 1 2 3 2 4 2 2 5 6 5 4 6 3 1 3 2 0 0	3 1 4 2 6 5 1 3 2

SOLUTION

graphs – topological sort

Algorithm analysis

In the problem it is necessary to perform topological sorting of the vertices of the directed graph.

Example

Consider the graphs presented in sample.

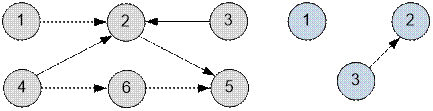
Possible topological sorts for the first graph are:

· 3, 1, 4, 2, 6, 5;

· 1, 3, 4, 6, 2, 5;

· 4, 1, 6, 3, 2, 5;

Algorithm realization

Declare the adjacency matrix of the graph g and the arrays used and top.

#define MAX 101

int g[MAX][MAX], used[MAX];

vector<int> top;

Function dfs performs a depth first search from the vertex v. Upon completion of processing the vertex v (when it becomes black), push it into the array top.

void dfs(int v)

{

used[v] = 1;

for (int i = 1; i <= n; i++)

if (g[v][i] && !used[i]) dfs(i);

top.push_back(v);

}

The main part of the program. Process several test cases.

while (scanf("%d %d", &n, &m), n + m > 0)

{

memset(g, 0, sizeof(g));

Read the input graph.

for (i = 0; i < m; i++)

{

scanf("%d %d", &a, &b);

g[a][b] = 1;

}

Initialize the arrays before processing the next test case.

memset(used, 0, sizeof(used));

top.clear();

Run the depth first search on a directed graph.

for (i = 1; i <= n; i++)

if (!used[i]) dfs(i);

Print the topological order of the vertices.

for (i = top.size() - 1; i >= 0; i--)

printf("%d ", top[i]);

printf("\n");

}

Java realization

import java.util.*;

public class Main

{

static int g[][], used[];

static ArrayList<Integer> top = new ArrayList<Integer>();

static int n, m;

static void dfs(int v)

{

used[v] = 1;

for (int i = 1; i <= n; i++)

if (g[v][i] == 1 && used[i] == 0) dfs(i);

top.add(v);

}

public static void main(String[] args)

{

Scanner con = new Scanner(System.in);

while(con.hasNextInt())

{

n = con.nextInt();

m = con.nextInt();

if (n + m == 0) break;

used = new int[n+1];

g = new int[n+1][n+1];

for (int i = 0; i < m; i++)

{

int a = con.nextInt();

int b = con.nextInt();

g[a][b] = 1;

}

top.clear();

for(int i = 1; i <= n; i++)

if (used[i] == 0) dfs(i);

for(int i = top.size() - 1; i >= 0; i--)

System.out.print(top.get(i) + " ");

System.out.println();

}

con.close();

}

}